LabVIEWでMandelbrot集合を描画する

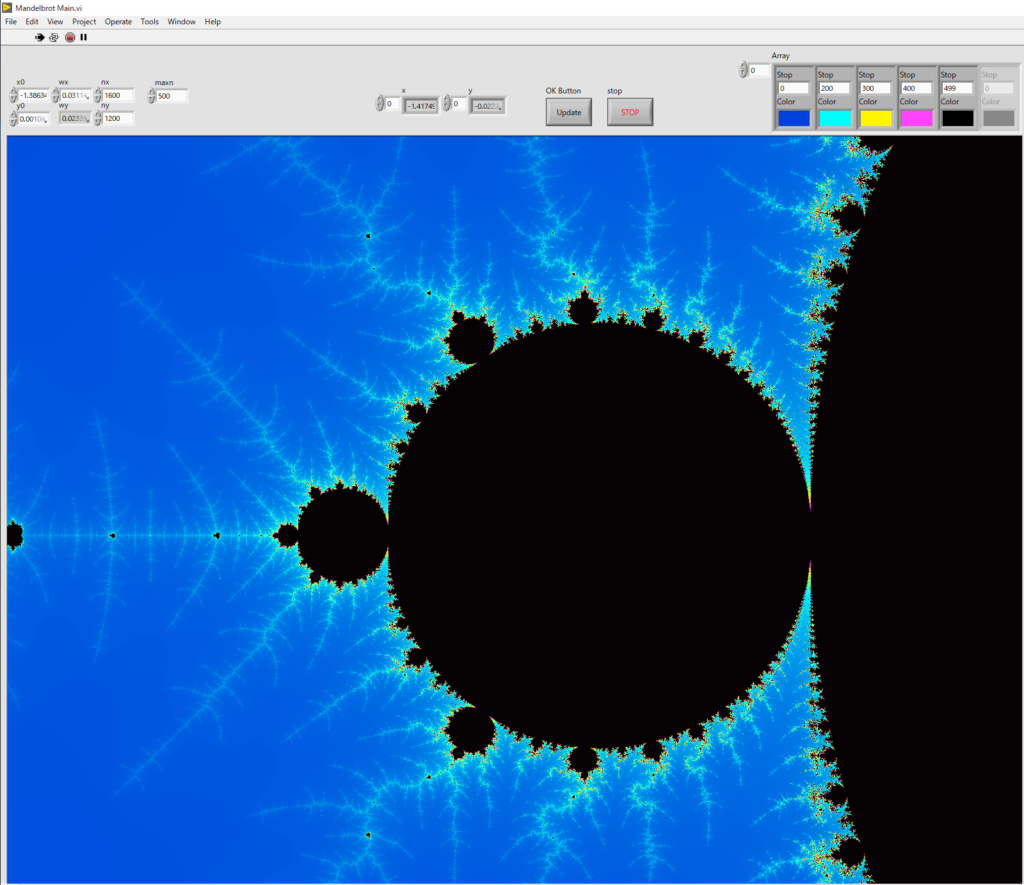
フラクタルな図形で有名で綺麗っぽいやつにMandelbrot(マンデルブロ)集合というのがある。どう言うのかというと

こういうやつである。高精細な画像を生成するにはそこそこのCPUスペックが必要であるため、かつてはベンチマークにも使用されたらしいが、今はCPUも早いので上記程度であればさほど時間がかからずに計算できる。今日はこれをLabVIEWで実装したので紹介する。

Mandelbrot集合とは

複素平面上の点cに対し、漸化式

を考える。このとき

でないcの集合をMandelbrot集合という。つまり、n→∞の極限で収束するようなcをいう。

漸化式を解くVIの作成

まずはこの漸化式を解き、発散するかどうかを考えるVIを作る。入力は複素数cであり、N回ループを回してznが発散するかを確認する。数学的な議論により

そうである。また、これを画像生成に落とし込むに当たって、発散の「速さ」を定義する

ただし、計算上無限回のループを行うことはできないため、ループの最大回数をN回に制限し、それまでに発散しなかった場合はk=Nとする。これを実装すると以下の様になる。

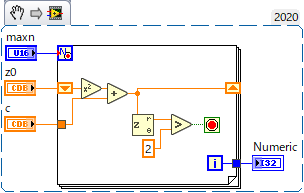
漸化式はシフトレジスタで表現する。Forループにある[▼]がそれであり、[▼]と[▲]をペアで使う。最初は[▼]にはz0が入る。最初のループではそのままForループの中身が実行され（z0^2+c）、右側の[▲]に入っていく。2回目のループでは前回のループで右側の[▲]に書き込まれた中身がそっくりそのまま左側の[▼]から読み出せる。このようにループの中で前回の値を参照しつつ、次の値を更新するといった場合にシフトレジスタを利用する。漸化式にもってこいというわけだ。

なお、LabVIEWでは直接複素数を扱うことができるため、何も考えず単に2乗し、cを足すだけで良い。複素数が扱えない言語の場合は自分で実部と虚部を計算する必要がある。Forループ中央にあるz,r,eとある部分は複素数を極座標（絶対値と偏角）に変換するVIであり、このうち絶対値が2を超えた場合Forループから抜けるようになっている。数列が収束しないときはループがN回まわるため、数値としてはN-1が収束の「速さ」として出力される。なお、高速化のためには、znの値が変化しなくなった場合や振動を始めた場合に即座にループを抜けることが有効であるが、簡単のためここでは省略した。

画像生成部分の作成

VIをサブVI化し、入力である複素数cを複素平面上で２次元的に変化させながら収束の速さを２次元カラープロットすれば画像が生成できる。LabVIEWには2次元カラープロット（＝２次元の数値配列を数値の大小に応じて各ピクセルに色を割り当てた画像として表示したグラフ）を表示するcontrol/indicator(制御器/表示器)としてIntensity Graphというものが存在するのでこれを使う。Block diagram上では2次元数値配列として見えるので、生成した二次元配列を接続するだけで基本的には良い。

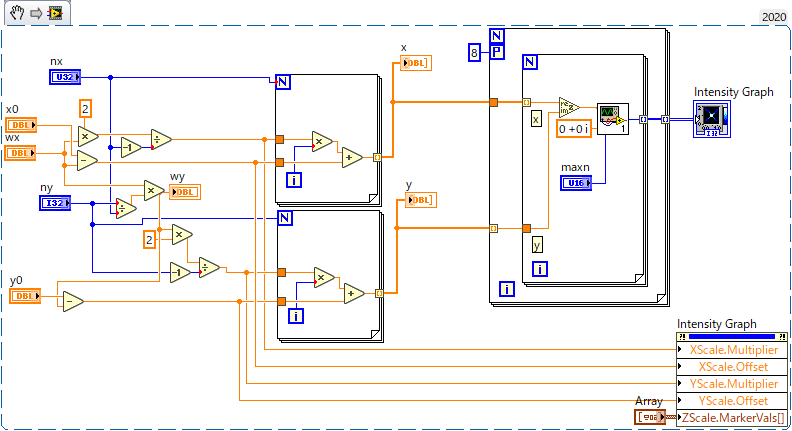
重要なのは右側の二重ループであり、ここで複素数をc=x+iyという感じで生成し、収束の速さをIndexing terminalでためておき、Intensity graphに書き込んでいる。前段は画像のピクセル数、描画領域の幅、描画領域の中心位置からx,y座標の配列を生成する段であり、あまり本質的ではない。右下のProperty nodeはIntensity GraphのXY軸範囲、カラーマップを指定するために必要だ。なお、Intensity Graphは右クリックメニューからTransposeをONにし、XとY軸のLoose fitをOFFにしないと思ったように表示されない

また、２重Forループの外側にPという端子がついている。これは並列実行を行うための設定をしているために表示されている。この場合、8コアを使用し、8並列で計算するように指定している。これを動作させるためには、サブVIのプロパティから再帰的実行を許可する設定が必要となる。

参考：https://zone.ni.com/reference/en-XX/help/371361R-01/lvconcepts/reentrancy/

全体像

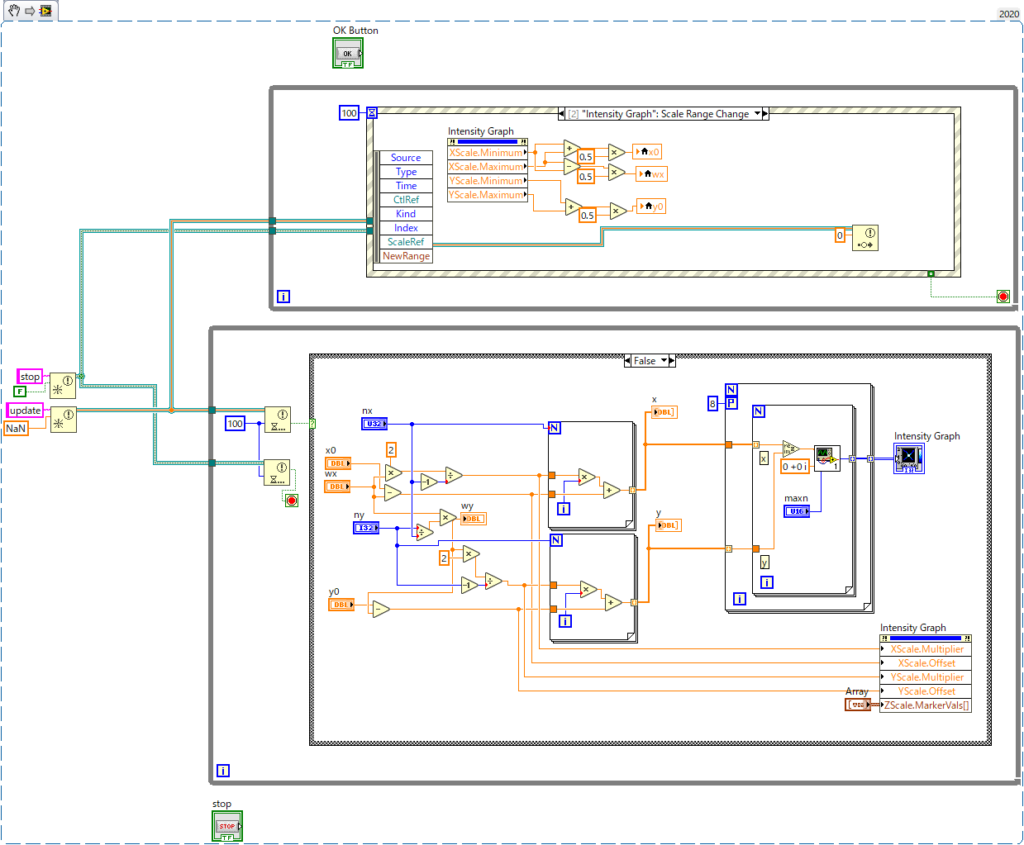
Graph Paletteの拡大縮小操作に反応するように雑に作ったのが以下。あまり綺麗じゃないが動けば良いと言うことでご容赦願いたい

[ダウンロード] (ZIP 45KB, MIT license)